On May 15, 2024, Professor Jian Liu and co-workers of the College of Chemistry and Molecular Engineering (CCME), Peking University published a letter entitled “Nonadiabatic Field with Triangle Window Functions on Quantum Phase Space”in The Journal of Physical Chemistry Letters. The Letter reports the nonadiabatic field (NaF) approach with triangle window functions (NaF-TW) on quantum phase space for studying nonadiabatic transition dynamics. It introduces new phase space expressions for time correlation functions based on triangle window functions for the NaF approach. The NaF-TW methodis expected to provide a more reliable practical tool for investigating nonadiabatic transitions in light-driven or electron/hole transfer processes in both natural and artificial complex molecular systems.
In nonadiabatic transition processes, the time scales of electronic and nuclear motionsare not separable, which presents the theoretical challenge for computer simulations of large systems. The category of mean-field methods in the spirit of the Ehrenfest theorem is not able to effectively describe the bifurcation of nuclear motion in the asymptotic region where the nonadiabatic coupling between electronic states vanishes. Another category of surface hopping methods with Born-Oppenheimer trajectories fails to capture the characteristic behavior, especially in broad nonadiabatic coupling regions where relatively short timescales are involved.
Since 2016, the Liu group has published a series of papers on the extension of the phase space representation of quantum mechanics for describing nonadiabatic transition processes.They have developed the constraint coordinate-momentum phase space (CPS) to represent discrete electronic degrees of freedom (DOFs) and described continuous nuclear DOFs with Wigner phase space. This framework treats electronic and nuclear DOFs equally, providing a rigorous foundation for phase space representations. Compared with conventional phase space representations for discrete DOFs, CPS avoids numerical instability and inefficiency. The Liu group suggests the three key elements of trajectory-based dynamics methods: (1) the equations of motion, (2) the initial condition, and (3) the integral expression for the expectation of the time-dependent physical quantity of interest. The unified quantum phase space framework offers a rigorous tool for dealing with the three key elements. Recently, it led to the development of the nonadiabatic field approach, which practically and faithfully captures the dynamical correlation between nuclear and electronic DOFs in both the asymptotic region and broad nonadiabatic coupling region for nonadiabatic transition processes in complex molecular systems.
More recently, the Liu group has employed the CPS representation along with non-covariant phase space functions, time-dependent weight functions, time-dependent normalization factors, and the Abel integral equation to construct a novel class of isomorphic representations for the exact dynamics of two-state systems (TSS). In such a class, the contribution of each trajectory to the population-population correlation function is strictly positive semi-definite. Interestingly, the triangle window function method, which was originally proposed as an empirical model, has been proven as an exact representation of the population dynamics of the TSS.
Since the triangle window function approach satisfies the positive semi-definite property of the population dynamics and is exactly isomorphic to the population dynamics of two-state systems, the Liu group employsthe CPS representation and the triangle window functions to develop a new formulation of electronic correlation functions for arbitrary finite-state systems. The combination with NaF, i.e., the NAF-TW approach, overcomes the limitations of various nonadiabatic dynamics methods with independent trajectories and offers a reasonably accurate tool for studying nuclear and electronic motion in nonadiabatic transition processes. It is capable of faithfully describing both nuclear and electronic dynamics in both the asymptotic region and the broad nonadiabatic coupling region from gas-phase to condensed-phase molecular systems.
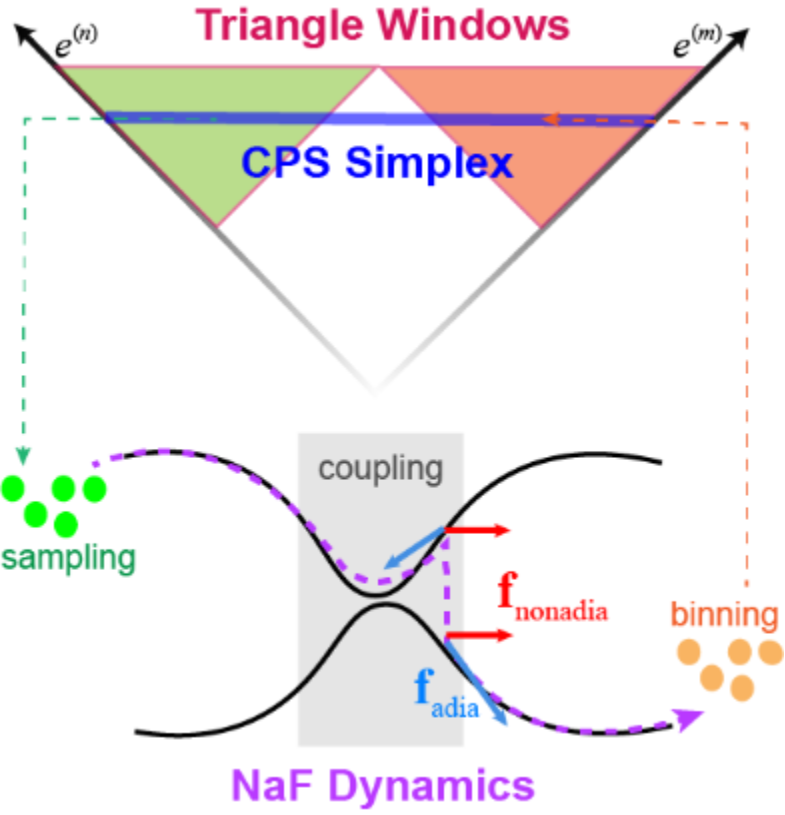
Fig. 1 Schematic representation fo rthe nonadiabatic field with triangle window functions (NaF-TW).

Fig. 2 For the condensed-phase two-state models, we compare the results of NaF-TW, SQC-TW, NaF (using CPS), Ehrenfest dynamics, and fewest switches surface hopping (FSSH). (a) shows the dynamics of the population difference of the spin-boson model, (b) displays the dynamics of the off-diagonal elements of the density matrix of the spin-boson model, and (c) presents the population dynamics results of the two-level atom-cavity model.
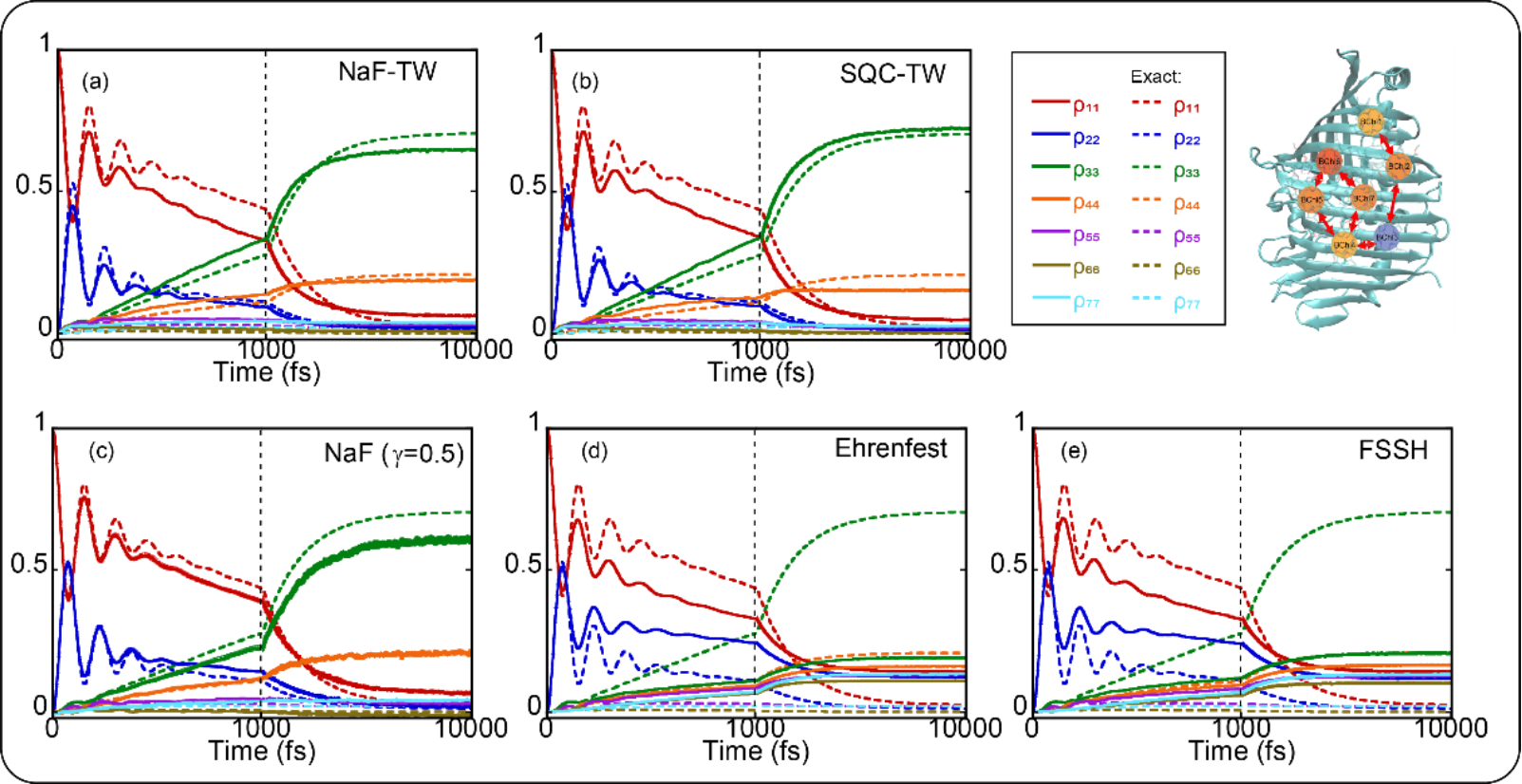
Fig. 3 Results of the population dynamics of the seven-state FMO model. Panels (a)-(e) display the results of NaF-TW, SQC-TW, NaF (using CPS), Ehrenfest dynamics, and FSSH, respectively.
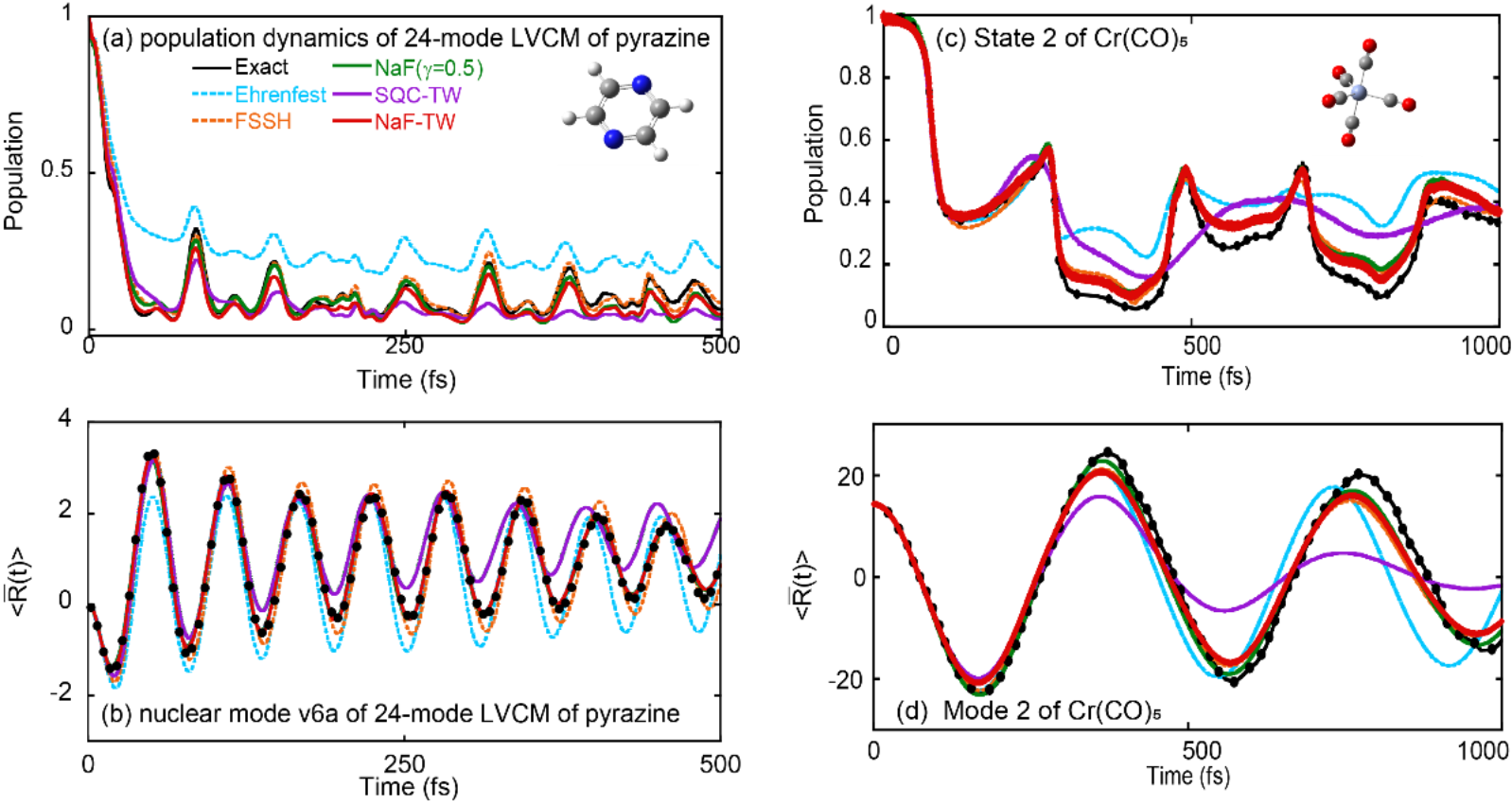
Fig. 4 Panels (a)-(b) show the population dynamics results and the time evolution of the expected values of normal mode positions for the 24-mode-2-state pyrazine molecule duringthe process around the conical intersection. Panels (c)-(d) do so for the 3-state Cr(CO)5 molecule during the conical intersection process. In Panels (a)-(d), the results of NaF-TW, SQC-TW, NaF (using CPS), Ehrenfest dynamics, and FSSH are exhibited.
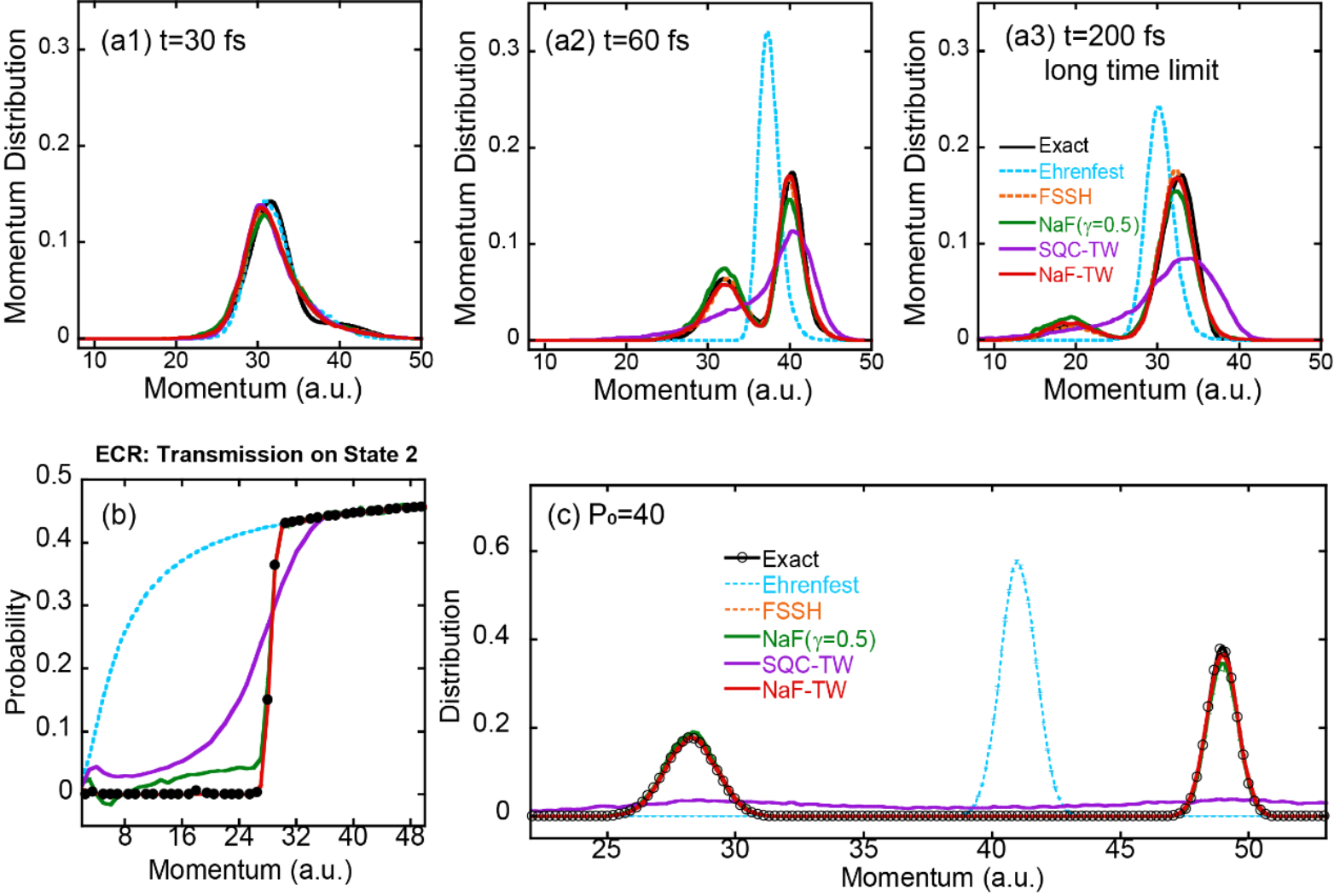
Fig. 5 Panels (a1)-(a3) show the distributions of nuclear momentum at t=30fs, 60fs, and 200fs of the three-state photodissociation modelby NaF-TW, SQC-TW, NaF (using CPS), Ehrenfest dynamics, and FSSH. Panel (b) depicts the probability of transmission on the second state for Tully's ECR scattering model by the same methods as in panel (a). Panel (c) presents the asymptotic nuclear momentum distribution for the initial momentum P0=40a.u. of the center of the initial momentum distribution for Tully's ECR scattering model for the same methods as in panel (a).
Figs. 2 and 3 provide comparisonsof different trajectory-based nonadiabatic methods for condensed-phase systems. NaF and NaF-TW exhibit notably superior performance compared totraditional methods such as Ehrenfest dynamics and FSSH in the simulation of time correlation functions for variousmodels. Fig. 4 illustrates the comparison of different nonadiabatic dynamics methods for studying the conical intersection model of real molecules. It suggests that NaF, NaF-TW, and FSSH perform better than SQC-TW and Ehrenfest dynamics. Lastly, Fig. 5 presents numerical results of different methods for a gas-phase nonadiabatic scattering model. It illustrates that NaF-TW is superior to the category of mean field trajectory-based methods (e.g., Ehrenfest dynamics and SQC-TW) in describing nuclear motion.
In summary, the Liu group has proposed the NaF-TW method on quantum phase space, which satisfies the positive semi-definiteness of electronic population in the adiabatic representation, and more importantly, overcomes the limitations of traditional nonadiabatic methods based on mean-field dynamics or surface hopping dynamics. NaF-TW is more consistent in theory and exhibits superior numerical performance in a suite of benchmark tests from gas-phase to condensed-phase. NaF-TW is promising for providing new reliable and effective tools in understanding and predicting important nonadiabatic transition phenomena in natural or artificial complex molecular systems.
Prof. Jian Liu is the corresponding author of the letter, and three co-authors are Xin He, Xiangsong Cheng, and Baihua Wu, three graduate students of CCME. This work was supported by the National Science Fund for Distinguished Young Scholars (Grant No. 22225304). We acknowledge the High-Performance Computing Platform of Peking University, Beijing PARATERA Tech Co., Ltd., and Guangzhou Supercomputer Center for providing computational resources.
Paper Information
“Nonadiabatic Field with Triangle Window Functions on Quantum Phase Space”
Xin He, Xiangsong Cheng, Baihua Wu, Jian Liu*. The Journal of Physical Chemistry Letters. 2024, 15, 5452–5466
https://doi.org/10.1021/acs.jpclett.4c00793
Related paper:
“A Novel Class of Phase Space Representations for the Exact Population Dynamics of Two-State Quantum Systems and the Relation to Triangle Window Functions”
Xiangsong Cheng, Xin He, Jian Liu*. Chinese Journal of Chemical Physics. 2024, 37, 230–254
https://doi.org/10.1063/1674-0068/cjcp2403033
https://cjcp.ustc.edu.cn/hxwlxb/en/article/doi/10.1063/1674-0068/cjcp2403033